The transformer is a key player in AC electrical power systems. It plays its role in stepping up right from generation again steps down the power on the other side while serving for primary and secondary distributions. For understanding the working of transformers you obviously need to understand the mathematics behind its working. Given below are the top ten formulas for transformers:
Turns ratio
Turns ratio is the ratio of primary turns to secondary turn. It is denoted by symbol ‘a’
Turns ratio Formula: a = Np / Ns
Related problem:
Problem 1: A certain transformer has 100 turns of wire on the primary side and 5 turns of wire on the secondary side. Find the turns ratio
Turns ratio = a = Np/Ns = 100/5 = 20
Voltage and turns ratio
The number of turns on the primary and secondary side is related to the turns ratio in the following manner:
Np/Ns = Vp(t)/Vs(t)
In simple terms a = Vp(t)/Vs(t)
where Vp(t) = AC voltage on primary side
Vs(t) = AC voltage on secondary side
Let’s solve a related problem
For problem 1, If 30 volts are applied on primary what will be the secondary voltage.
Solution: Np/Ns = Vp(t)/Vs(t);
100 / 5 = 30 / Vs(t)
Vs(t) = 30 * 5 / 100 = 1.5 volts
Current and turns ratio
The current and turns ration on a transformer are related by the following formula:
Np/Ns = Is(t)/Ip(t)
For problem 1, If we apply 1.5 amps on primary what will be the secondary current
Np/Ns = Is(t)/Ip(t);
100/5 = Is(t)/1.5
Is(t) = 30 amps
Transformer kVA Calculation Formula
Three phase kVA can be calculated using following formula:
kVA = (1.732 * Eline * Iline) / 1000
Efficiency
Generally, Efficiency is expressed as the ratio of output to input voltage.
Mathematically,
Efficiency (η) = Pout/Pin
%age Efficiency (η) = (Pout/Pin) * 100%
where Pin = Pout + Plosses
where Plosses = PCu + PCore
and Pout = Vs.IsCosθs
Putting above parameters in transformer efficiency formula we have:
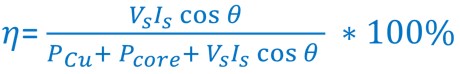
Single phase full load current
Current flowing through the transformer can be calculated using kVA to amps calculation formula:
In case of known VA: Single phase full load current = VA/Voltage
In case of known kVA: Single phase full load current = kVA/Voltage
Three phase full load current
KVA to Amps in case of three phase
I = kVA * 1000 / 1.73 * Voltage
Primary and Secondary Line current
Ip (line) = (kVA*1000)/(1.73*E(line))
Is (line) = (kVA*1000)/(1.73*E(line))
Impedance transformation
A transformer can change the apparent impedance of the element. Using a transformer it is possible to match the load impedance to source impedance. The formula for impedance transformation on the transformer is:
Z’L = a2ZL
Where Z’L = Apparent impedance of primary circuit
Voltage regulation
Voltage regulation formula compares the output voltage of transformer at no load to the voltage transformer at full load.
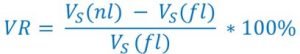
where
Vs (nl) = Secondary voltage at no load
Vs (fl) = Secondary voltage at full load
