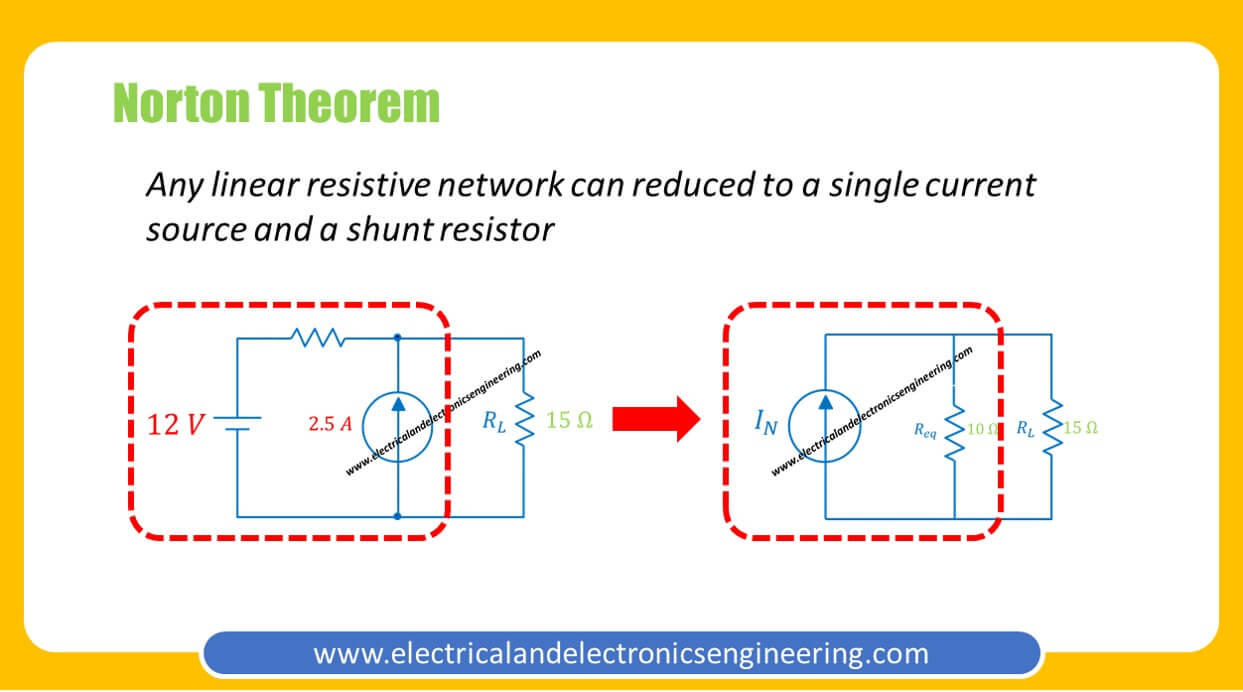
Norton’s theorem is a circuit analysis technique which is used to reduce complex electrical circuits to a single current source and one parallel resistor. Statement of Norton theorem:
Any linear bilateral network can be reduced to a simple circuit containing one current source and one shunt resistor
Given below are steps for Norton’s Theorem
- Replace all current zeros with open and all voltage sources with short
- Identify and remove the load from the circuit
- Label resulting terminals (We’ll label them x and y)
- Find the equivalent resistance
- Now again connect all sources
- Form a short circuit by connecting x and y
- Find current that flows through the circuit
- Connect current source (value obtained from step 6) to the shunt resistor (value obtained from step 4)
Example
Let’s solve an example for better understanding the Norton’s theorem
Consider the circuit given below:
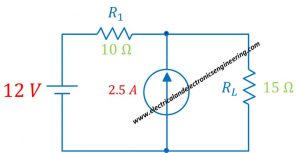
Problem statement: Replace the circuit by Norton equivalent circuit for load resistor of 15 ohms.
Step 1: First of all zero all sources. i.e Replace voltage source by short and current source by open.
Step 2: Remove the load resistor
Step 3: Label the resulting terminals as x and y
Step 4: Find equivalent resistance
Figure below illustrates step 1, 2, 3, and 4
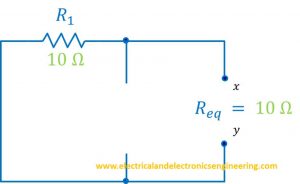
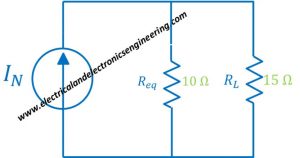
Here the equivalent resistance is 10 ohms
Step 5: Now again connect all sources to circuit:
Step 6: Short the terminals x and y
Step 7: Find the current flowing through short circuit
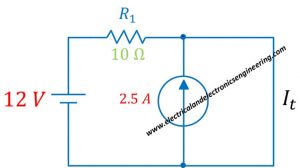
Since we have a circuit with multiple sources Superposition principle ideally suits the condition
Firstly replace current source and find current flowing through resistor:
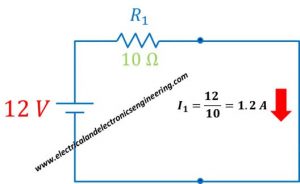
Now replace voltage source by short and apply current divider to find current through resistor

Since we have a short circuit the overall current will flow through the short
The overall current flowing through short is:
I (t) = I (1) + I (2) = 1.2 + 2.5 = 3.7 A
Step 8: Using Req from 4 and current from 7th step we obtain equivalent circuit as follows: