Nodal Analysis [Node Voltage Analysis]

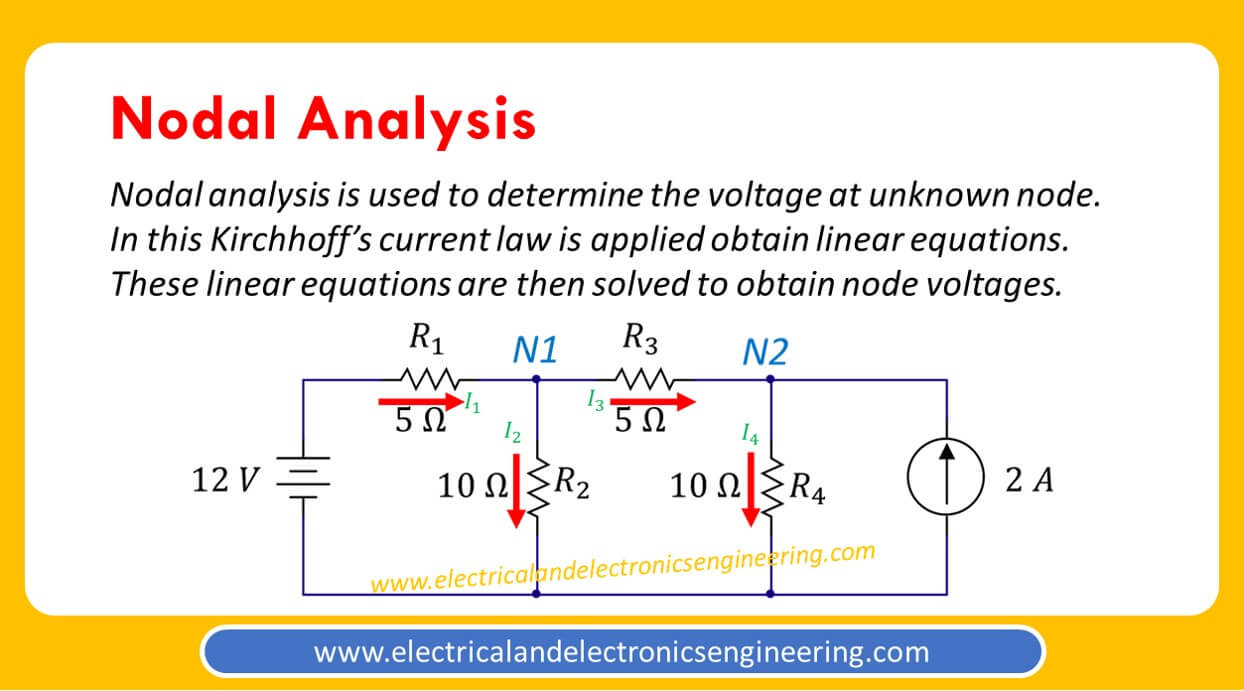
The nodal analysis is used to determine the potential different at any node with an arbitrary reference point.

In nodal analysis the Kirchhoff’ current law is applied to form linear equations. These linear equations are then solved to find the unknown voltages.

Steps for Nodal Analysis

1. Select a reference node and mark it as ground
2. Name remaining nodes
3. Label current through all passive elements
4. Apply Kirchhoff’s Current law to all nodes that are not connected to a voltage source
5. Solve the linear equations to obtain the unknown voltage sources

Solved Example

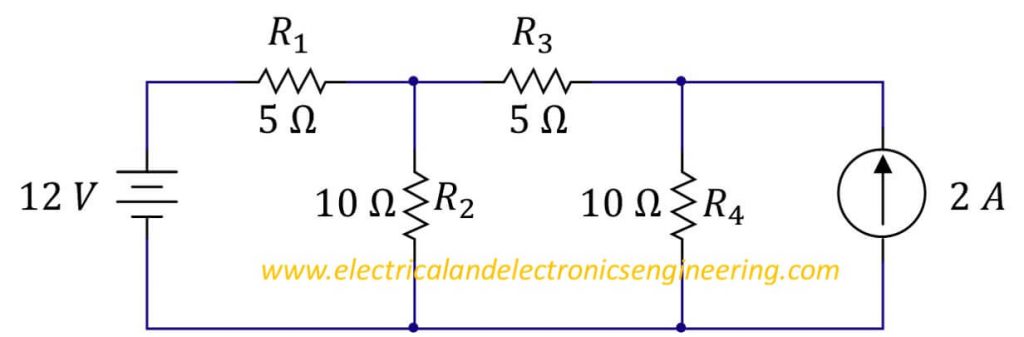
Step 1: Label the reference node

Step 2: In this circuit we have two nodes, naming them N1 and N2

Step 3: Labeling all passive elements (resistors)

After above steps we obtain following:

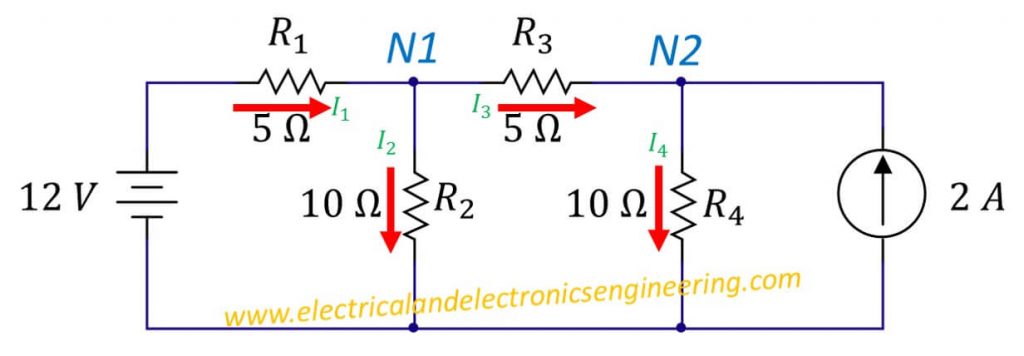
Step 4: Apply Kirchhoff’s Current Law at node N1. Let’s assume the voltage at node N1 is V1 and voltage at node N2 is V2.

I₁ = I₂ + I₃

From Ohm’s law above equation transforms to:

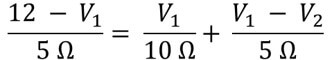
After solving above equation we have following linear equation:

5 V₁ – 2V₂ = 24 … (1)

Application of KVL on node 2 yields:

I₃ + 2A = I₄

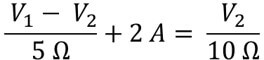
After solving above equation we have the following:

2 V₁ – 3V₂ = -20 … (2)

Step 5: Solving linear equations

After solving equation 1 and 2 we obtain:

V₁ = 10.18 V

V₂ = 13.455 V