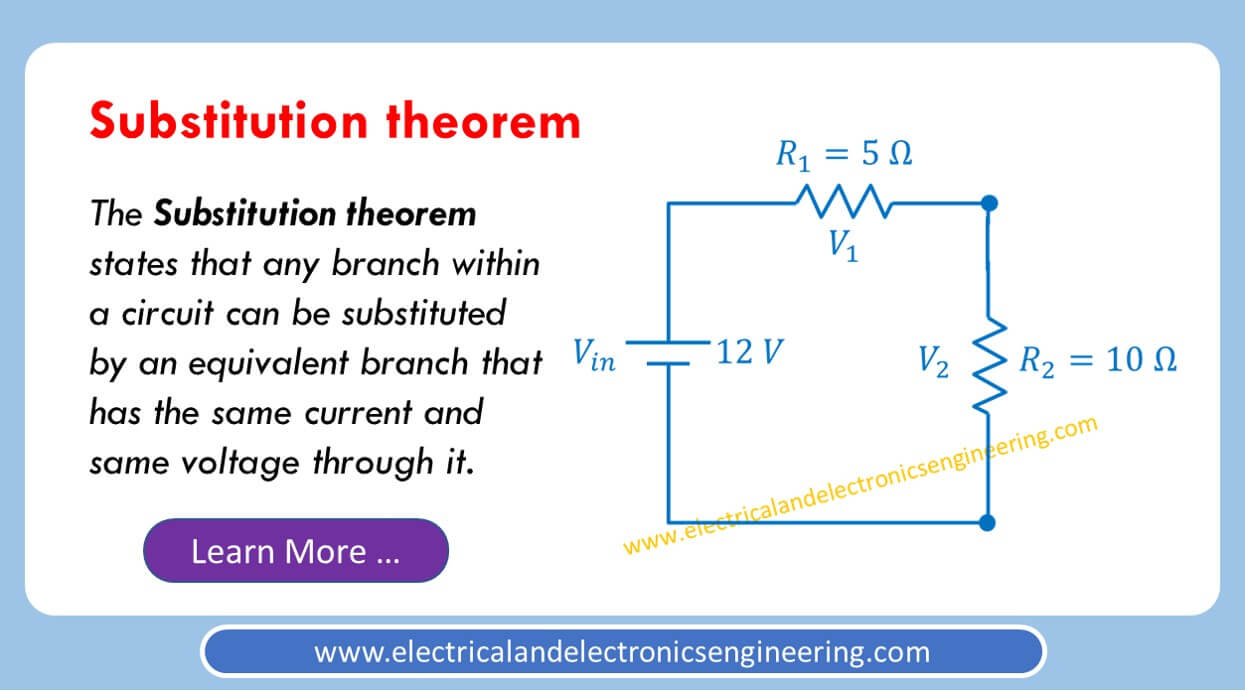
The substitution theorem states that any branch within a circuit can be substituted by an equivalent branch that has the same current and same voltage through it.
Illustration:
Consider a series circuit containing two resistors: 10 ohms and 5 ohms connected to a 12 v source. From voltage divider rule, the Resistor R1 has 4 V drop across it while resistor R2 has a drop of 8 Volts across it:
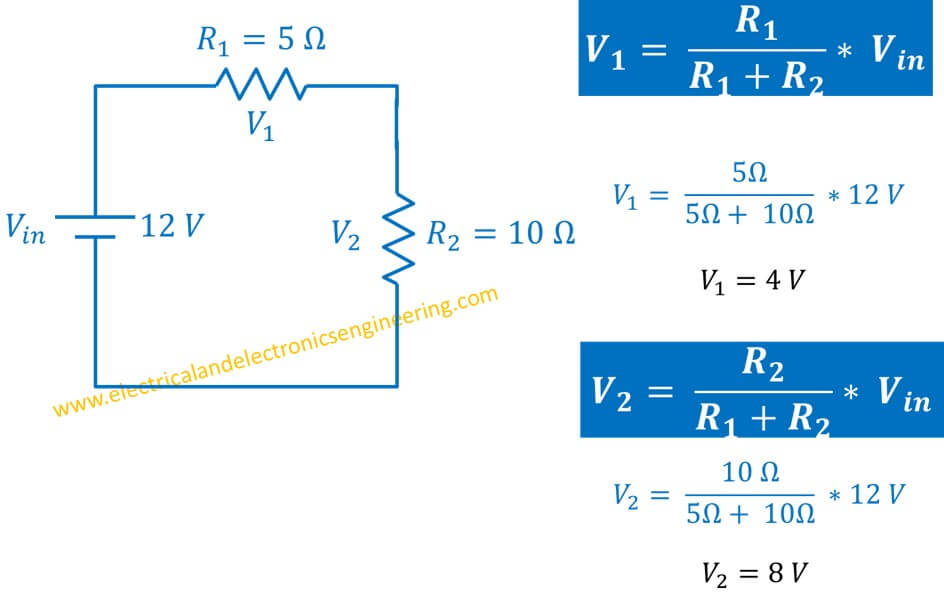
From Ohm’s law, the current passing through 10 ohms resistor is:
I = V/R = 8 V / 10 Ω = 0.8 A
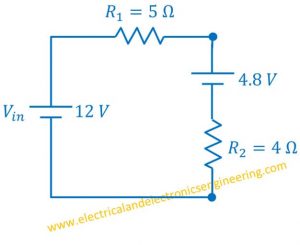
According to substitution theorem, the resistor R2 can be replaced by any combination of components that fulfills our condition of 0.8 A current and a voltage drop of 8 volts across it.
For instance, the resistor R2 which is now 10 ohms can be replaced by a resistor of 4 ohms provided and a series voltage drop of 4.8 v. The current through the circuit is still 0.8 Amps
Example: Replace the resistor R2 in the same circuit with 200 mA current source pointing upward and a shunt resistor.
Solution: To maintain the same current in the circuit, the branch current should stay the same. However, we need to apply Kirchhoff’s current law to find the current across the shunt resistor.
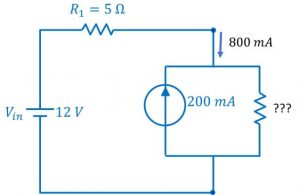
Now unknown current (???),
I = 800 mA + 200 mA = 1 A
Voltage across 5 ohms resistor = 5 ohms * 800 mA = 4000 mA = 4 V
From Kirchhoff’s Voltage law rest all voltage (8 V) will be dissipated across the branch is 8 volts.
To maintain 8 volts @ 1 Amps we need to have a resistance of 8 ohms:
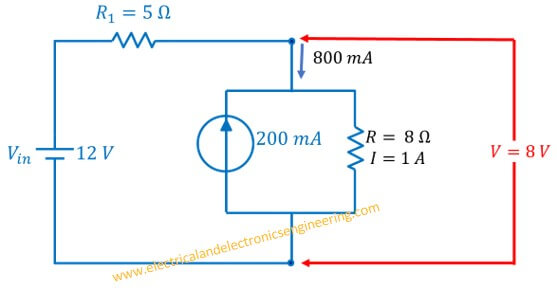
So we need a 200 mA current source pointing upward and a shunt source of 8 ohms to obtain substituted circuit.