Mesh analysis or loop analysis involves the application of Kirchhoff’s voltage law to a circuit. KVL provides linear equations which are used to obtain current in branches.
5 Steps to Apply Mesh Analysis
- Assign a clockwise current direction to all loops in a network
- Label the loops and indicate the voltage polarity
- Apply Kirchhoff’s voltage law to the loops (Any resistor common to two loops will have two voltage drops)
- Application of KVL will yield simultaneous equations that should be solved
- Branch currents that are common to a branch are algebraically determined by combining the loop currents
An Example
Let’s solve an example to better understand this.
Consider the circuit below:
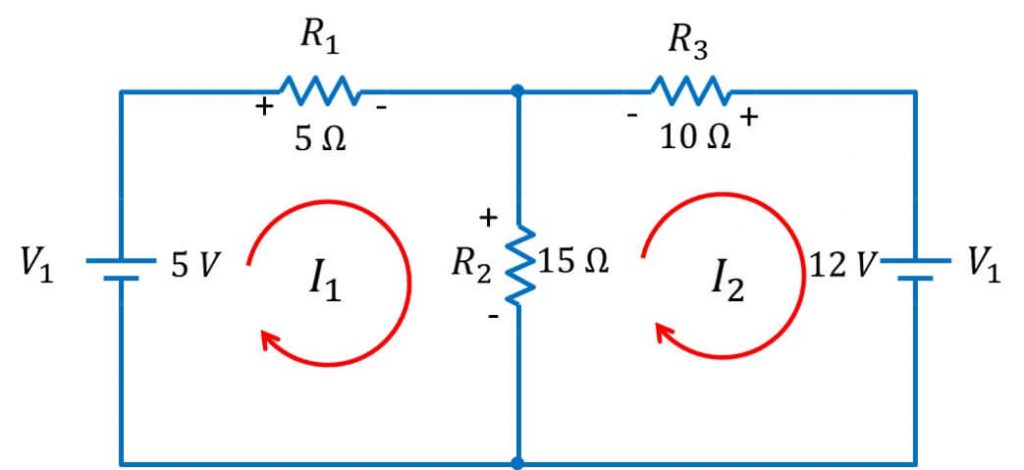
Apply Kirchhoff’s voltage law in the left loop:
V(1) = V(R1) + V(R2)
5 V = 5 Ω * I1 + 15 Ω ( I1 – I2)
5 V = I1 (5 + 15) – 15 I2
20 I1 – 15 I2 = 5 … Eqn(1)
Apply Kirchhoff’s voltage law in right loop:
V(R2) + V(R3) + V(2) = 0
15 Ω ( I2 – I1) + 10 Ω I2 + 12 V = 0
15 I1 – 25 I2 = 12 … Eqn(2)
Solving these two equations we have:
I1 = -0.2 A
I2 = -0.6 A
Negative symbol in both equations indicate that actual current is flowing in opposite direction.